今回は、G検定【ディープラーニングの概要】の「ディープラーニングとニュートラルネットワーク」の解説についてです。
(前の記事:G検定の過去問対策【機械学習1】具体的手法:教師あり学習と教師なし学習)
AI(人工知能)を実用化できたのは、このディープラーニングのお陰だと言われています。
ここでは、用語の解説だけでなく、数学の関数、導関数や微分が苦手な人へ、概念を簡単に解説しています。
本文の内容は、G検定の公式テキストの内容を主に参照し、文系の私が自分でもわかり易いように追記しています。

Contents
ディープラーニングとニューラルネットワークの違いとは
ディープラーニングとニューラルネットワークの違いについて説明します。
【ディープラーニング】とは
ディープラーニングとは、ニューラルネットワークを応用した手法です。
この手法のモデル自体は、ディープニューラルネットワークと呼ばれることが大半です。
あくまでも機械学習と同様に人工知能の研究分野を指します。
ディープラーニングは、一言でいえば「隠れ層」を増やしたネットワークです。
層が多い、つまり層が「深い」ことから、別名「深層学習」とも呼ばれます。
上記はあくまでもディープラーニングの基本形であり、現在はこの基本形以外にも様々なモデルが考えられています。
【ニューラルネットワーク】とは
ニューラルネットワークとは、人間の脳の中にある「ニュートロンのネットワーク」を模しているので、ニューラルネットワークと呼ばれています。
入力と出力の関係性が、隠れ層の中に重みとして表現されているのに過ぎません。
隠れ層は、入力を受け取り、出力を吐き出す、入力と出力を対応づける関数に相当しています。
入力と出力を吐き出す数学の関数とは
関数は、数式で表されます。
現代的には数の集合に値をとる写像の一種であると理解される。
(引用:wikipedia より)
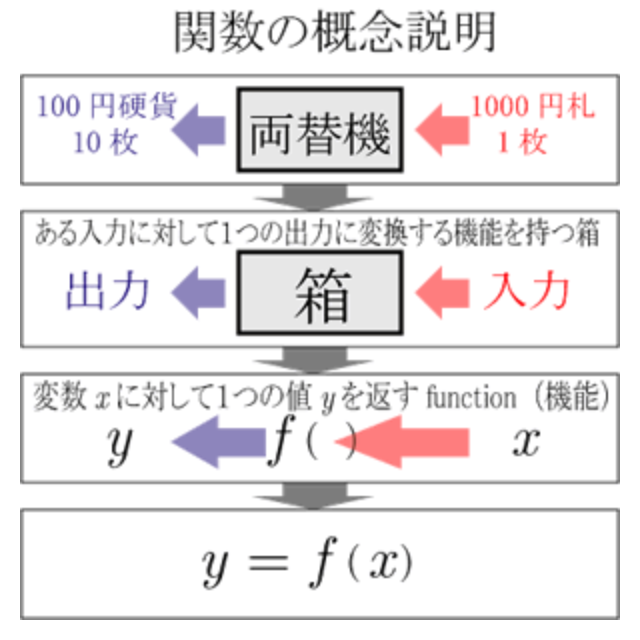
(引用画像:「KIT数学ナビゲーション」より)
AI(人工知能)は、数学の数式の理解も必要です。
ニューラルネットワークの基本形【多層パーセプトロン】とは
隠れ層が無いニューラルネットワーク「単純パーセプトロン」もあります。
これは、線形分類しか行うことができず、非常に単純な関数しか表現できません。
新たに「関数」を追加することで、非線形分類ができるようになりました。
これが多層パーセプトロンです。
【多層パーセプトロン (Multi-Layer Perceptron : MLP)】
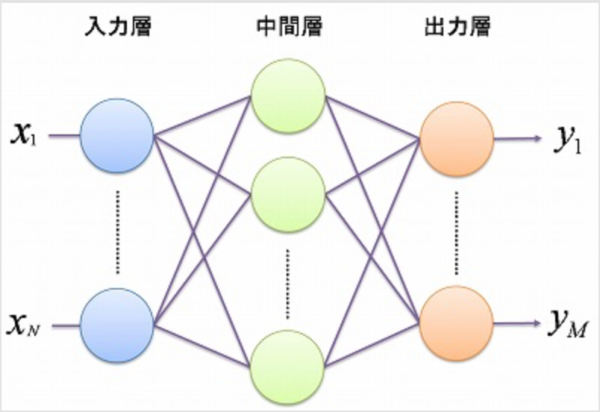
(画像引用:ifs.nog.cc より)
既存のニューラルネットワークの問題
ディープラーニングで実践される「隠れ層」を増やすアイデアは、良いアイデアのようですが、長年、実用化できませんでした。
その理由は、「隠れ層」を単純に増やしただけのニュートラルネットワークでは、「誤差逆伝播法」の問題が起こるからです。
「誤差逆伝播法」とはアルゴリズムの1つで、機械学習でニューラルネットワークを学習させる際に用いられます。
【誤差逆伝播法のイメージ】
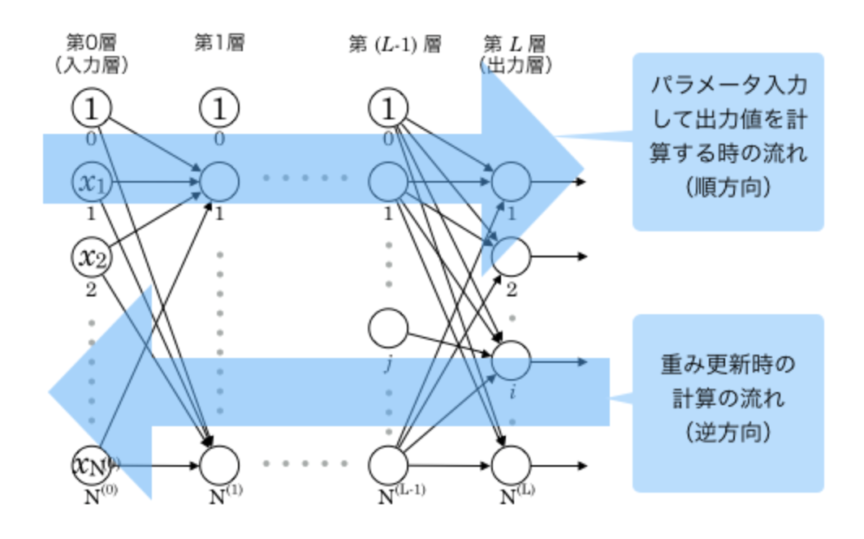
(画像引用:高卒でもわかる機械学習より)
モデルの予想結果と実際の正解値との誤差をネットワークに逆向きにフィードバックさせる形でネットワークの重みを更新することです。
誤差が正確にフィードバックできなくなります。
よって「隠れ層」によりネットワークが深くなると、誤差が最後まで正しく反映されなくなる結果が出て、モデルの精度が上がるどころか、大きく下がります。
「隠れ層」を増やすと問題が起きる原因
隠れ層を増やすと誤差のフィードバックが上手くいかなくなる大きな原因の一つが「シグモイド関数」の特性です。
シグモイド関数とは、単調増加連続関数で1つの変曲点を持ち、モデルの出力に使われます。

(引用:Wikipediaより)
誤差はネットワークを逆向きに順々に伝播していきます。
その数式の過程で、もともとの誤差に幾つかの項が掛け合わされます。
原因になる項の一つが「活性化関数の微分」です。
活性関数とは、ニューロンに集まった入力信号をどのように活性化するかを決定する関数です。
【活性関数のイメージ】
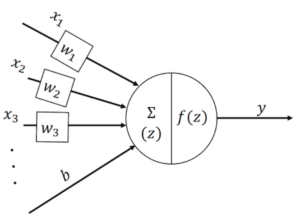
(画像引用:Renomより)
微分係数と導関数は、「定数なのか、関数なのか」という違いがあります。
微分した関数(導関数)は、下図のようになります。

(画像引用:イメージングソリューションより)
シグモイド関数の微分は最大値が0.25にしかならず、これは1よりも小さいです。
0.25は1よりもかなり小さいので、伝播していく誤差は、隠れ層を遡るごとに、どんどん小さくなります。
その結果、多くの隠れ層があると、入力層付近の隠れ層に到達するまでには、フィードバックするべき誤差がなくなります。
この問題は勾配消失問題と呼ばれ、ニューラルネットワークを深層にするときに、大きな妨げになります。
以上の問題から、人工知能の分野でディープラーニングが登場するまでは、ニューラルネットワークは、人気のない手法でした。
次は「ディープラーニング」が、ニューラルネットワークの問題を解決する手法について紹介します。
文系がAI(人工知能)時代に生き残るために、G検定は、知識を身につけるに最も役立ちます。


